Project

kalman_filter

0.01
No commit activity in last 3 years
No release in over 3 years
kalman_filterjjviscomi/kalman-filterHomepageDocumentationSource CodeBug TrackerWiki
Noisy sensor data, approximations in the equations that describe the system evolution, and external factors that are not accounted for all place limits on how well it is possible to determine the system's state. The Kalman filter deals effectively with the uncertainty due to noisy sensor data and to some extent also with random external factors. The Kalman filter produces an estimate of the state of the system as an average of the system's predicted state and of the new measurement using a weighted average. The purpose of the weights is that values with better (i.e., smaller) estimated uncertainty are "trusted" more. The weights are calculated from the covariance, a measure of the estimated uncertainty of the prediction of the system's state. The result of the weighted average is a new state estimate that lies between the predicted and measured state, and has a better estimated uncertainty than either alone. This process is repeated at every time step, with the new estimate and its covariance informing the prediction used in the following iteration. This means that the Kalman filter works recursively and requires only the last "best guess", rather than the entire history, of a system's state to calculate a new state.
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
2017
2018
2019
2020
2021
2022
2023
2024
2025
 Popularity
Downloads
7,522
Stars
11
Forks
3
Watchers
2
 Releases
Current version
1.0.2
Total releases
3
First release
2016-11-06
Latest release
2016-11-07
 Issues
Open Issues
0
Closed Issues
1
Total Issues
1
Issue Closure Rate
100%
 Pull Requests
Open Pull Requests
0
Closed Pull Requests
0
Merged Pull Requests
2
Pull Request Acceptance Rate
100%
 Development
Primary Language
Ruby
Licenses
MIT
Average date of last 50 commits
2017-12-08
Reverse Dependencies
0

 Dependencies
 Project Readme

Gem Version

kalman_filter

A ruby implementation of a Kalman filter that is easy to use.

  • what is it

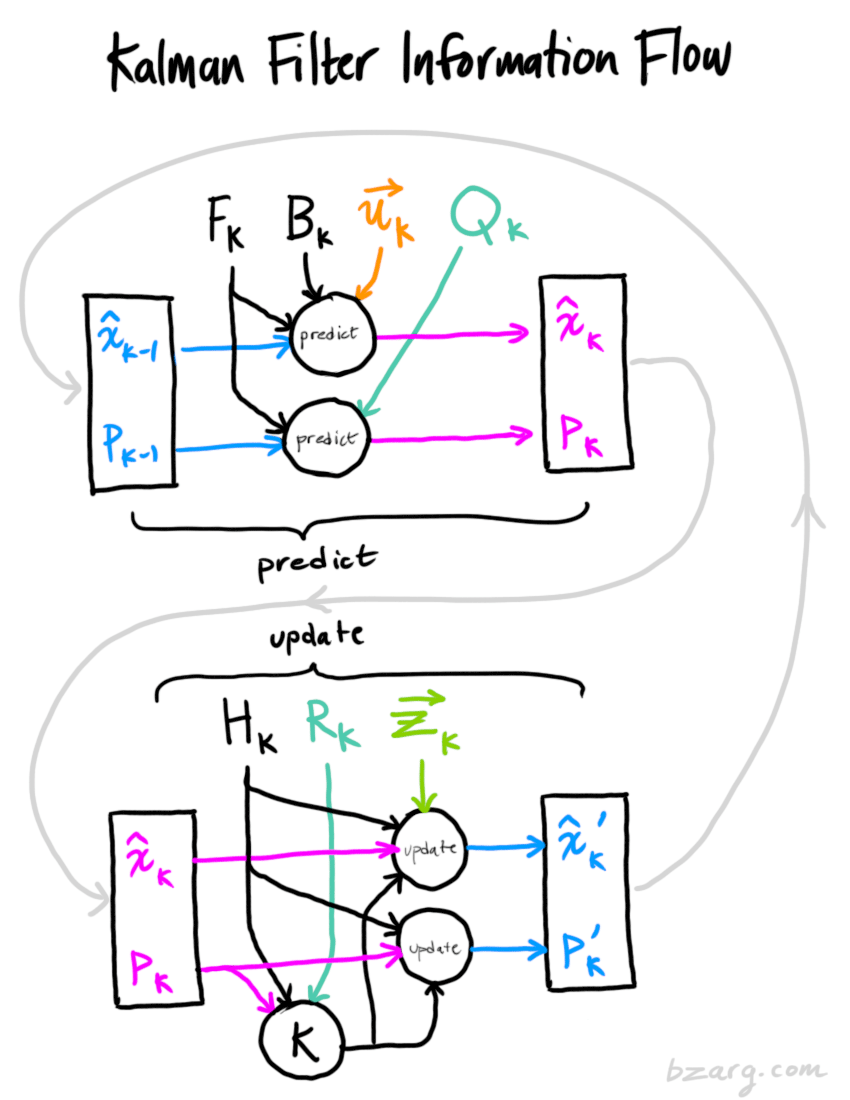
    You can use a Kalman filter in any place where you have uncertain information about some dynamic system, and you can make an educated guess about what the system is going to do next. Even if messy reality comes along and interferes with the clean motion you guessed about, the Kalman filter will often do a very good job of figuring out what actually happened. And it can take advantage of correlations between crazy phenomena that you maybe wouldn’t have thought to exploit!

Kalman filters are ideal for systems which are continuously changing. They have the advantage that they are light on memory (they don’t need to keep any history other than the previous state), and they are very fast, making them well suited for real time problems and embedded systems.

Image of KalmanFilter

install

gem install kalman_filter

or include it in your Gemfile

gem 'kalman_filter'

options

# process_noise: describes how much noise this system introduces.
# measurement_noise: describes how much noise is in the measurement itself.
# state_vector: describes how to transition from the current state to the next state.
# control_vector: describes how the filter changes given some other input.
  
kf = KalmanFilter.new process_noise: 0.005, measurement_noise: 0.5

use

require 'kalman_filter'

kf = KalmanFilter.new process_noise: 0.005, measurement_noise: 0.5

kf.measurement = 65     # records a new measurement into the filter, and returns the new value of the filter
# >> 65

kf.measurement = 72
# >> 72

kf.measurement          # returns the last measurement taken
# >> 72

kf.value                # returns the current value of the filter
# >> 69.67441860465117