A Ruby gem for manipulating and solving sliding tile puzzles.

(Also see sliding_puzzle_rust)

You might have come across sliding tile puzzles before. They're usually cheap, plastic-y toys that can be rearranged by sliding their tiles around. Here's an example containing a picture of a frog:

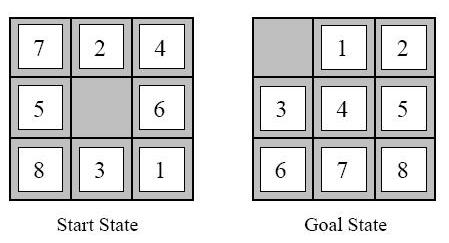
One of the pieces is blank which means an adjacent tile can move into its place. After repeating this a few times, these puzzles can be tricky to solve. We can also think of these puzzles as grids of numbers:

The challenge is to find a sequence of moves to rearrange the 'start state' into the 'goal state' in as few moves as possible. This gem lets you play with these puzzles and it solves them in an optimal number of moves.

In this example the blank is in the the upper-left corner of the goal state, but it's arbitrary where it's located.

Puzzles are represented as arrays of numbers:

puzzle = SlidingPuzzle.new(
  [1, 2, 0], # <-- the 0 represents blank
  [3, 4, 5],
  [6, 7, 8],
)

You can slide tiles around and print the result:

puzzle.slide!(:right)
puzzle.print
# [1, 0, 2]
# [3, 4, 5]
# [6, 7, 8]

The #slide method will return a new SlidingPuzzle whereas #slide! will mutate the existing one.

You can return an array of possible moves for a sliding puzzle:

puzzle = SlidingPuzzle.new(
  [1, 2, 0],
  [3, 4, 5],
  [6, 7, 8],
)

puzzle.moves
#=> [:right, :up]

If you try a move that isn't valid, an error is raised:

puzzle.slide(:left)
# SlidingPuzzle::InvalidMoveError, "unable to slide left"

You can scramble a puzzle:

puzzle.scramble!

By default, this will perform 100 random moves, but you can set this:

puzzle.scramble!(moves: 3)

The #scramble method will return a new SlidingPuzzle whereas #scramble! will mutate the existing one.

Puzzles can have different dimensions:

two_by_four = SlidingPuzzle.new(
  [1, 2, 3, 4],
  [5, 6, 7, 0],
)

two_by_four.slide!(:down)
two_by_four.print
# [1, 2, 3, 0]
# [5, 6, 7, 4]

Puzzles must be rectangular and contain a single blank.

Finding the shortest solution for a sliding puzzle is a hard problem. This gem provides 'oracles' to find these solutions:

goal_state = SlidingPuzzle.new(
  [1, 2, 0],
  [3, 4, 5],
  [6, 7, 8],
)

oracle = SlidingPuzzle.oracle(goal_state)

This 'oracle' finds the shortest solution from any start state:

start_state = SlidingPuzzle.new(
  [1, 4, 2],
  [3, 7, 5],
  [6, 0, 8],
)

oracle.solve(start_state)
#=> [:down, :down, :left]

Oracles aren't magic. They are the result of precomputing solutions in advance. This gem provides oracles for puzzles with up to eight tiles:

goal_state = SlidingPuzzle.new(
  [1, 2, 3, 4],
  [5, 0, 6, 7],
)

oracle = SlidingPuzzle.oracle(goal_state)

The numbers of the goal state must be sequential, but the blank can be anywhere.

The #oracle method will return nil for a puzzle with more than eight tiles, or if the numbers aren't sequential.

Some starting positions are impossible to solve. For example, if you swap any two tiles from the goal state, there's no way to solve the puzzle:

unsolvable = SlidingPuzzle.new(
  [2, 1, 0],
  [3, 4, 5],
  [6, 7, 8],
)

oracle.solve(unsolvable)
#=> nil

In total, there are N! possible configurations for a puzzle with N tiles (including the blank), but only half of these are solvable.

For the 3x3 puzzle, there are 9! / 2 = 181,400 solvable configurations.

For dimensions with no oracles, you can precompute your own:

goal_state = SlidingPuzzle.new(
  [0, 1,  2, 3],
  [4, 5,  6, 7],
  [8, 9, 10, 11],
)

oracle = SlidingPuzzle.precompute(goal_state)

You can then write the result to a file:

oracle.write("path/to/file")

And read it in later:

oracle = SlidingPuzzle.read("path/to/file")

start_state = SlidingPuzzle.new(
  [1, 5,  2,  3],
  [4, 0,  6,  7],
  [8, 9, 10, 11],
)

oracle.solve(start_state)
#=> [:down, :right]

For puzzles with greater than 12 tiles, you won't be able to precompute an oracle in a reasonable amount of time. The 4x4 puzzle will take more than 40,000 times longer to precompute than the 3x4 puzzle and require terrabytes of RAM. The debug flag will reveal if it's ever likely to finish:

SlidingPuzzle.precompute(goal_state, debug: true)
# queue size: 1
# queue size: 2
# queue size: 3
# ...

If it just keeps growing, it's unlikely to finish.

There are a few other methods that may be useful:

# Get the number on the first row and second column:
puzzle.get(0, 1)
#=> 5

# Find the row and column of the number 5:
puzzle.find(5)
#=> [0, 1]

# Return a clone of the array of tiles:
puzzle.tiles
#=> [[1, 5,  2,  3], [4, 0,  6,  7], [8, 9, 10, 11]]

# Return a clone of the puzzle:
puzzle.clone
#=> #<SlidingPuzzle:object_id>

I hope you have fun with this gem. Here are some things to try:

1. Find an algorithm to solve a puzzle without using an oracle
2. Compare the number of moves your algorithm makes with the oracle
3. Write a web server for interacting with sliding puzzles
4. Read more about techniques for coping with larger dimensions
5. Write a user interface to slide tiles around